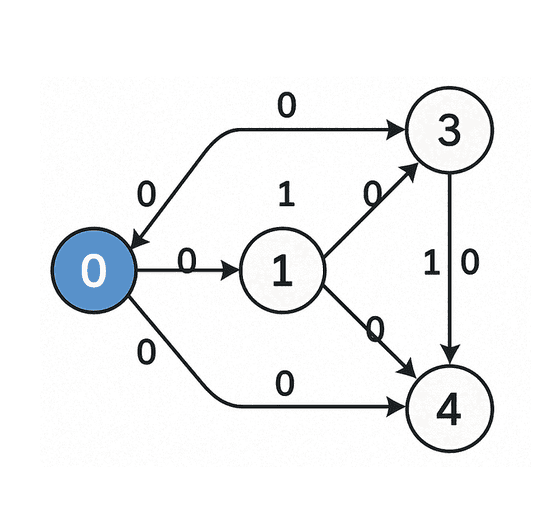
Zero One BFS Algorithm Intro

Intro

01 BFS is an efficient shortest path algorithm for graphs where edge weights are only 0 or 1

Special case of BFS/Dijkstras

Instead of using a standard priority queue, it uses a deque to achieve O(V + E) time

Efficiently computes shortest distances from a single source in such graphs

Graph Requirements

Weighted graph with edge weights only 0 or 1 only
Directed or Undirected
Represented Using:
- Adjacency List

Output

Shortest distance from the source node to all other nodes Optionally, the path itself

Video Animation

written: https://codeforces.com/blog/entry/22276

Pseudo Code

    from collections import deque

    def zero_one_bfs(graph, source):

        n = len(graph)
        dist = [float('inf')] * n
        dist[source] = 0

        dq = deque()
        dq.append(source)

        while dq:
            node = dq.popleft()
            for neighbor, weight in graph[node]:
                if dist[node] + weight < dist[neighbor]:
                    dist[neighbor] = dist[node] + weight
                    if weight == 0:
                        dq.appendleft(neighbor)  # 0-weight edges prioritized
                    else:
                        dq.append(neighbor)      # 1-weight edges go to back

        return dist

Time Complexity

Each vertex is processed at most once Each edge is considered at most once

Must faster than Dijkstras for this specific case O(E + V) instead of O(E log V)

Space Complexity

Distance Array: O(V) Deque: O(V) in worst case

IRL Use Case

Special Graphs Slide (0 cost) vs Step (1 cost)
Network Propagation With Free/Paid Edges 0 for instance transfer, 1 for delayed transfer

2290. Minimum Obstacle Removal to Reach Corner ::1:: - Hard

Topics: Array, Breadth First Search, Graph Theory, Heap (Priority Queue), Matrix, Shortest Path

Intro

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values: 0 represents an empty cell, 1 represents an obstacle that may be removed. You can move up, down, left, or right from and to an empty cell. Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).

Example Input	Output
grid = [[0,1,1],[1,1,0],[1,1,0]]	2
grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]	0

Constraints:

m == grid.length

n == grid[i].length

1 ≤ m, n ≤ 10^5

2 ≤ m*n ≤ 10^5

grid[i][j] is either 0 or 1

grid[0][0] == grid[m-1][n-1] == 0

Abstraction

Given a graph full of empty cell or obstacles, determine the minimum number of obstacles to remove to move from top left to bottom right

Space & Time Complexity

Solution	Time Complexity	Space Complexity	Time Remark	Space Remark

Bug	Error

Brute Force:

Aspect	Time Complexity	Space Complexity	Time Remarks	Space Remarks

Find the Bug:

Solution 1: [01 BFS] 01 BFS Approach - Advanced Graphs/Advanced Graphs

    def minimumObstacles(self, grid: List[List[int]]) -> int:
        # Grid dimensions
        m, n = len(grid), len(grid[0])

        # Directions: up, down, left, right
        directions = [(1,0), (-1,0), (0,1), (0,-1)]

        # distance matrix: min obstacles removed to reach each cell
        dist = [[float('inf')] * n for _ in range(m)]
        dist[0][0] = grid[0][0]  # starting cost (remove if starting on 1)

        # deque for 0-1 BFS
        dq = deque()
        dq.append((0,0))

        while dq:

            r, c = dq.popleft()

            # Explore neighbors
            for dr, dc in directions:
                nr, nc = r + dr, c + dc

                # Valid boundaries
                if 0 <= nr < m and 0 <= nc < n:

                    # New distance = current + cost to enter neighbor
                    new_dist = dist[r][c] + grid[nr][nc]

                    # Relaxation
                    if new_dist < dist[nr][nc]:
                        dist[nr][nc] = new_dist

                        # 0-cost move → appendleft
                        if grid[nr][nc] == 0:
                            dq.appendleft((nr, nc))
                        # 1-cost move → append to back
                        else:
                            dq.append((nr, nc))

        # Result: min obstacles to remove to reach bottom-right
        return dist[m-1][n-1]

1368. Minimum Cost to Make at Least One Valid Path in a Grid ::1:: - Hard

Topics: Array, Breadth First Search, Graph Theory, Heap (Priority Queue), Matrix, Shortest Path

Intro

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be: 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1]) 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1]) 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j]) 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j]) Notice that there could be some signs on the cells of the grid that point outside the grid. You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest. You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only. Return the minimum cost to make the grid have at least one valid path.

Example Input	Output
grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]	3
grid = [[1,1,3],[3,2,2],[1,1,4]]	0
grid = [[1,2],[4,3]]	1

Constraints:

m == grid.length

n == grid[i].length

1 ≤ m, n ≤ 100

1 ≤ grid[i][j] ≤ 4

Abstraction

What the heck!

Space & Time Complexity

Solution	Time Complexity	Space Complexity	Time Remark	Space Remark

Bug	Error

Brute Force:

Aspect	Time Complexity	Space Complexity	Time Remarks	Space Remarks

Find the Bug:

Solution 1: [01 BFS] 01 BFS Approach - Advanced Graphs/Advanced Graphs

    def minCost(self, grid):
        m, n = len(grid), len(grid[0])
        
        # directions: right, left, down, up
        dirs = [(0,1), (0,-1), (1,0), (-1,0)]
        
        # visited[i][j] = minimum cost to reach (i,j)
        visited = [[float('inf')] * n for _ in range(m)]
        visited[0][0] = 0
        
        dq = deque()
        dq.append((0,0,0))  # i, j, cost
        
        while dq:
            i, j, cost = dq.popleft()
            
            for d, (dx, dy) in enumerate(dirs, start=1):
                ni, nj = i + dx, j + dy
                
                if 0 <= ni < m and 0 <= nj < n:
                    # If we follow the arrow, cost = 0; otherwise cost = 1
                    new_cost = cost if d == grid[i][j] else cost + 1
                    
                    if new_cost < visited[ni][nj]:
                        visited[ni][nj] = new_cost
                        if d == grid[i][j]:
                            dq.appendleft((ni, nj, new_cost))  # 0-cost → front
                        else:
                            dq.append((ni, nj, new_cost))      # 1-cost → back
        
        return visited[m-1][n-1]

LeetCode: Graphs II 01 BFS