LeetCode: Graphs II Hierholzers Eulers
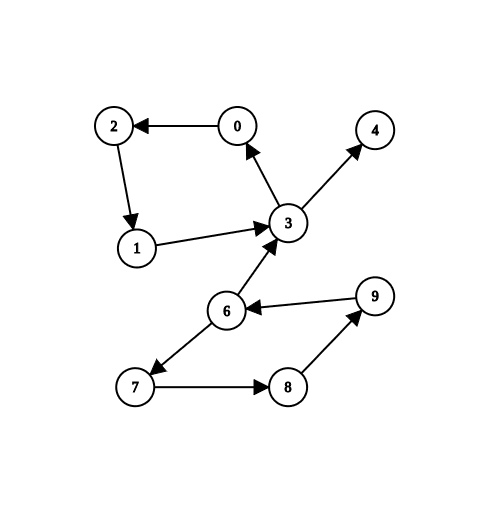
Table Of Contents
Hierholzers Algorithm Intro
Graph Requirements
Output
Video Animation
Hierholzers: https://www.youtube.com/watch?v=qZrfK2iE4UA
Pseudo Code
Time Complexity
Space Complexity
IRL Use Case
What is Hierholzers Algorithm
332. Reconstruct Itinerary ::1:: - Hard
Topics: Depth First Search, Graph, Eulerian Circuit
Intro
You are given a list of airline tickets where tickets[i] = [fromi, toi] represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it. All of the tickets belong to a man who departs from "JFK", thus, the itinerary must begin with "JFK". If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"]. You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.
| Example Input | Output |
|---|---|
| tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]] | ["JFK","MUC","LHR","SFO","SJC"] |
| tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]] | ["JFK","ATL","JFK","SFO","ATL","SFO"] |
Constraints:
1 ≤ tickets.length ≤ 300
tickets[i].length == 2
fromi.length == 2
toi.length == 3
fromi and toi consist of uppercase English letters.
fromi != toi
Abstraction
Given a graph, determine the flight path.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: [Hierholzer's] [Eulerian Path] Hierholzer's Algorithm Eulerian Path via DFS + MinHeap for Lexical Order - Advanced Graphs/Advanced Graphs
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
# Hierholzer's Algorithm / DFS on Graphs:
# Hierholzer is similar to DFS on trees, but adapted for graphs with cycles.
# Key differences:
# 1. DFS on Trees:
# - Visits each node exactly once
# - Appends nodes in post-order (after visiting children)
# - No cycles, so edges are implicitly used exactly once
# 2. Hierholzer DFS on Graphs:
# - Visits each edge exactly once (nodes can be visited multiple times)
# - Removes edges as they are used to prevent revisiting
# - Appends nodes in post-order after all outgoing edges are traversed
# - Handles cycles and constructs Eulerian paths or circuits
# 3. Analogy:
# - Tree DFS explores nodes, Hierholzer DFS explores edges
# - Post-order ensures correct construction of paths in both
# Result:
# - DFS-like traversal that builds a valid Eulerian path using every edge exactly once
# Hierholzer’s Algorithm:
# Designed to construct an Eulerian path efficiently.
# Core Idea:
# - Recursively follow edges, removing them as you go, using each edge exactly once.
# - PostOrder Construction: append airports after visiting all outbound edges,
# so the path is built in reverse.
# - Lexical Order Preserved: if multiple edges exist, minHeap allows to choose the smallest airport
# Eulerian Path:
# A trail in a graph that visits every edge exactly once, allowing for revisiting vertices.
# - In the context of flight tickets:
# - Each ticket represents a directed edge from one airport to another.
# - We must use all tickets exactly once, starting from "JFK".
# - We are allow to revisit airports
# Graph Existence rules:
# 1. At most: one node has (out-degree - in-degree) = 1 (starting node)
# 2. At most: one node has (in-degree - out-degree) = 1 (ending node)
# 3. All other nodes have equal degrees (in-degree == out-degree).
# Directed Graph (Adjacency List):
# - Vertices: airports
# - Edges: flight tickets (from src -> dest)
# - Neighbors: destinations reachable from a given airport
# - MinHeap ensures lexical order when multiple choices exist
# Note:
# 1. Build graph: graph[src] = MinHeap of destinations
# (MinHeap ensures lexical order when multiple choices exist)
# 2. Use DFS to traverse graph:
# Always choose the smallest lexical destination first
# Remove tickets (edges) as we use them
# 3. Append airports to itinerary in post-order (after visiting neighbors/edges)
# 4. Reverse itinerary at the end to get correct order starting at JFK
# Result -> shortest path through all airports starting at jfk
# Build adjacency list with MinHeaps
# sc: O(V), number of vertices
graph = defaultdict(list)
# Build MinHeap for each source airport
# sc: O(E), one entry per edge used
for src, dest in tickets:
heapq.heappush(graph[src], dest)
# itinerary build in reverse (post order)
# sc: O(E), one entry per edge used
itinerary = []
def dfs(airport):
# Explore all neighbors in lexical order
# tc: each edge processed once -> O(E)
while graph[airport]:
# tc: O(log E) per pop
next_dest = heapq.heappop(graph[airport])
dfs(next_dest)
# PostOrder append to itinerary
# sc: O(1) per append, overall O(E)
itinerary.append(airport)
# Start Eulerian Path via DFS + MinHeap from "JFK"
# tc: O(E log E) for all recursive DFS calls with heap pops
dfs("JFK")
# Reverse to get correct order
# tc: O(E), sc: O(E) for reversed list
res = itinerary[::-1]
# overall: tc O(e log e)
# overall: sc O(e + v)
return res