LeetCode: Graphs II A Star Heuristic
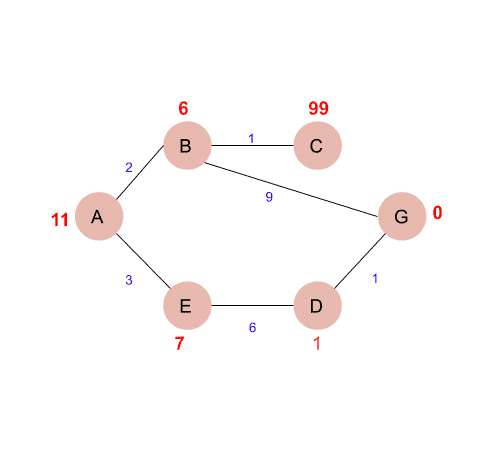
Table Of Contents
A Star Heuristic Algorithm Intro
Graph Requirements
Output
Video Animation
A Star Heuristic: https://www.youtube.com/watch?v=71CEj4gKDnE
Pseudo Code
Time Complexity
Space Complexity
IRL Use Case
What is A Star Heuristic Algorithm
1002. Network Delay Time ::1:: - Medium
Topics: Depth First Search, Breadth First Search, Graph, Heap (Priority Queue), Shortest Path
Intro
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target. We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
| Example Input | Output |
|---|---|
| times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 | 2 |
| times = [[1,2,1]], n = 2, k = 1 | 1 |
| times = [[1,2,1]], n = 2, k = 2 | -1 |
Constraints:
1 ≤ k ≤ n ≤ 100
1 ≤ times.length ≤ 6000
times[i].length == 3
1 ≤ ui, vi ≤ n
ui != vi
0 ≤ wi ≤ 100
All the pairs (ui, vi) are unique. (i.e., no multiple edges.)
Abstraction
Given a graph, each node with 1 edges, determine how much time is needed to get from start node to target node.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: [Dijkstra's] BFS And MinHeap To Keep Shortest Path - Advanced Graphs/Advanced Graphs
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# Dijkstra's Algorithm (Single-Source Shortest Path):
# We want the minimum time for a signal sent from node k
# to reach all n nodes in a directed graph with non-negative weights.
# Key Ideas:
# 1. Model the network as a directed weighted graph.
# 2. Use a min-heap to always expand the node with the smallest
# known signal arrival time.
# 3. Maintain a dictionary of shortest known times to each node.
# 4. If all nodes are reached, return the maximum of these times.
# 5. If some node is unreachable, return -1.
# Build adjacency list: graph[src] = [(dest, weight), ...]
# tc: O(edge)
graph = defaultdict(list)
for u, v, w in times:
graph[u].append((v, w))
# Min-Heap:
# Each entry is (time_to_reach_node, node)
# sc: O(node)
heap = [(0, k)]
# Dictionary to track shortest known time to each node
# Invariant: once a node is added here, its shortest time is finalized
shortest_time = {}
# tc: each node/edge O(e) processed via O(log n) heap operations O(e log n)
while heap:
# Pop node with smallest known arrival time
time, node = heapq.heappop(heap)
# Skip if this node already has a finalized shortest time
# (We found a better path earlier)
if node in shortest_time:
continue
# Record shortest time to reach this node
shortest_time[node] = time
# Explore Choices:
# Relax all outgoing edges from this node
for neighbor, wt in graph[node]:
# If neighbor not finalized, push updated time candidate
if neighbor not in shortest_time:
heapq.heappush(heap, (time + wt, neighbor))
# After processing:
# If not all nodes were reached, signal cannot reach everyone
if len(shortest_time) != n:
return -1
# Result:
# The total network delay is the maximum shortest arrival time
res = max(shortest_time.values())
# overall: tc O(e log n)
# overall: sc O(n + e)
return res